Многомерное шкалирование

Многомерное шкалирование

Общая цель
Логика многомерного шкалирования
Вычислительные методы
Задание размерности пользователем
Интерпретация осей координат
Приложения
Многомерное шкалирование и факторный анализ

Общая цель

Общая цель

Многомерное шкалирование (МНШ) можно рассматривать как альтернативу факторному анализу (см. Факторный анализ). Целью последнего, вообще говоря, является поиск и интерпретация "латентных (т.е. непосредственно не наблюдаемых) переменных", дающих возможность пользователю объяснить сходства между объектами, заданными точками в исходном пространстве признаков. Для определенности и краткости, далее, как правило, будем говорить лишь о сходствах объектов, имея ввиду, что на практике это могут быть различия, расстояния или степени связи между ними. В факторном анализе сходства между объектами (например, переменными) выражаются с помощью матрицы (таблицы) коэффициентов корреляций. В методе МНШ дополнительно к корреляционным матрицам, в качестве исходных данных можно использовать произвольный тип матрицы сходства объектов. Таким образом, на входе всех алгоритмов МНШ используется матрица, элемент которой на пересечении ее i-й строки и j-го столбца, содержит сведения о попарном сходстве анализируемых объектов (объекта [i] и объекта [j]). На выходе алгоритма МНШ получаются числовые значения координат, которые приписываются каждому объекту в некоторой новой системе координат (во "вспомогательных шкалах", связанных с латентными переменными, откуда и название МНШ), причем размерность нового пространства признаков существенно меньше размерности исходного (за это собственно и идет борьба).

В начало

Логика многомерного шкалирования

Логика многомерного шкалирования

Логику МНШ можно проиллюстрировать на следующем простом примере. Предположим, что имеется матрица попарных расстояний (т.е. сходства некоторых признаков) между крупными американскими городами. Анализируя матрицу, стремятся расположить точки с координатами городов в двумерном пространстве (на плоскости), максимально сохранив реальные расстояния между ними.
Полученное размещение точек на плоскости впоследствии можно использовать в качестве приближенной географической карты США.

В общем случае метод МНШ позволяет таким образом расположить "объекты" (города в нашем примере) в пространстве некоторой небольшой размерности (в данном случае она равна двум), чтобы достаточно адекватно воспроизвести наблюдаемые расстояния между ними. В результате можно "измерить" эти расстояния в терминах найденных латентных переменных. Так, в нашем примере можно объяснить расстояния в терминах пары географических координат Север/Юг и Восток/Запад.

Ориентация осей координат.
Ориентация осей координат.

Как и в Факторном анализе, ориентация осей может быть выбрана произвольной. Возвращаясь к нашему примеру, можно поворачивать карту США произвольным образом, но расстояния между городами при этом не изменятся. Таким образом, окончательная ориентация осей на плоскости или в пространстве является, в большей степени результатом содержательного решения в конкретной предметной области (т.е. решением пользователя, который выберет такую ориентацию осей, которую легче всего интерпретировать). В примере можно было бы выбрать ориентацию осей, отличающуюся от пары Север/Юг и Восток/Запад, однако последняя удобнее, как "наиболее осмысленная" и естественная.

В начало

Вычислительные методы

Вычислительные методы

Многомерное шкалирование - это не просто определенная процедура, а скорее способ наиболее эффективного размещения объектов, приближенно сохраняющий наблюдаемые между ними расстояния. Другими словами, МНШ размещает объекты в пространстве заданной размерности и проверяет, насколько точно полученная конфигурация сохраняет расстояния между объектами. Говоря более техническим языком, МНШ использует алгоритм минимизации некоторой функции, оценивающей качество получаемых вариантов отображения.

Меры качества отображения:
Меры качества отображения:

стресс. Мерой, наиболее часто используемой для оценки качества подгонки модели (отображения), измеряемого по степени воспроизведения исходной матрицы сходств, является так называемый стресс.

Величина стресса Phi в для текущей конфигурации определяется так:

Phi =

[dij - f (

ij)]2

Здесь dij - воспроизведенные расстояния в пространстве заданной размерности, а

ij (дельтаij) - исходное расстояние. Функция f (

ij) обозначает неметрическое монотонное преобразование исходных данных (расстояний). Таким образом, МНШ воспроизводит не количественные меры сходств объектов, а лишь их относительный порядок.

Обычно используется одна из несколько похожих мер сходства. Тем не менее, большинство из них сводится к вычислению суммы квадратов отклонений наблюдаемых расстояний (либо их некоторого монотонного преобразования) от воспроизведенных расстояний. Таким образом, чем меньше значение стресса, тем лучше матрица исходных расстояний согласуется с матрицей результирующих расстояний.

Диаграмма Шепарда.
Диаграмма Шепарда.

Можно построить для текущей конфигурации точек график зависимости воспроизведенных расстояния от исходных расстояний. Такая диаграмма рассеяния называется диаграммой Шепарда. По оси ординат OY показываются воспроизведенные расстояния (сходства), а по оси OX откладываются истинные сходства (расстояния) между объектами (отсюда обычно получается отрицательный наклон). На этом график также строится график ступенчатой функции. Ее линия представляет так называемые величины D-с крышечкой, то есть, результат монотонного преобразования f(

) исходных данных. Если бы все воспроизведенные результирующие расстояния легли на эту ступенчатую линию, то ранги наблюдаемых расстояний (сходств) был бы в точности воспроизведен полученным решением (пространственной моделью). Отклонения от этой линии показывают на ухудшение качества согласия (т.е. качества подгонки модели).

В начало

Задание размерности пользователем

Задание размерности пользователем

Если вы уже знакомы с факторным анализом, вы вполне можете пропустить этот раздел. В противном случае вы можете перечитать раздел Факторный анализ. Однако это не является необходимым для понимания идей многомерного шкалирования.

Вообще говоря, чем больше размерность пространства, используемого для воспроизведения расстояний, тем лучше согласие воспроизведенной матрицы с исходной (меньше значение стресса). Если взять размерность пространства равной числу переменных, то возможно абсолютно точное воспроизведение исходной матрицы расстояний. Однако нашей целью является упрощение решаемой задачи, с тем, чтобы объяснить матрицу сходства (расстояний) в терминах лишь нескольких важнейших факторов (латентных переменных или вспомогательных шкал). Возвращаясь к нашему примеру с расстояниями между городами, если получена двумерная карта, намного проще представить себе расположение городов и планировать передвижение между ними, чем если бы имелась только матрица попарных расстояний.

Причины плохого качества отображения.
Причины плохого качества отображения.

Обсудим, почему уменьшение числа факторов (или вспомогательных шкал) может приводить к ухудшению представления исходной матрицы. Обозначим буквами A, B, C и D, E, F две тройки городов. Соответствующие им точки и попарные расстояния между ними показаны в двух табличках (матрицах).

A B C D E F A
B
C D
E
F

0
90
90

0
90

0
90
180

0
90

Первой матрице соответствует случай когда города удалены друг от друга в точности на 90 километров, а второй - когда города D и F удаляются на 180 километров. Можно ли три точки, соответствующие городам (объектам) расположить в одномерном пространстве (на прямой)? Действительно, три точки, соответствующие городам D, E и F могут быть расположены на прямой линии:

D---90 км---E---90 км---F

D удален на 90 км от города E, и E - на 90 км от F, а город D удален на 90+90=180 км от F. Если попытаться проделать тоже самое с городами A, B и C, то видно, что соответствующие им точки уже нельзя разместить на прямой с сохранением исходной структуры расстояний. Однако эти точки можно расположить на плоскости, например, в виде треугольника:

A
90 км		90 км
B	90 км	C

Располагая эти три точки так, можно в точности воспроизвести все расстояния между ними.

Без лишних деталей, этот пример показывает, как конкретная матрица расстояний (сходств) связана с числом искомых латентных переменных (размерностью результирующего пространства). Конечно, "реальные" данные никогда не являются такими "точными", и содержат случайный шум, т.е. случайную изменчивость, влияющую на различие между воспроизведенной и исходной матрицей.

Критерий "каменистой осыпи".
Критерий "каменистой осыпи".

Обычно, для выбора размерности пространства, в котором будет воспроизводится наблюдаемая матрица, используют график зависимости стресса от размерности (график каменистой осыпи). Этот критерий впервые был предложен Кэттелом (Cattell (1966)) в контексте решения задачи снижения размерности в факторном анализе (см. Факторный анализ); Краскал и Виш (Kruskal and Wish (1978; стр. 53-60)) обсуждали применение этого графика в методе МНШ.

Кэттел предложил найти такую абсциссу на графике (в методе ФА, по оси абсцисс идут собственные значения), в которой график стресса начинает визуально сглаживаться в направлении правой, пологой его части, и, таким образом, уменьшение стресса максимально замедляется. Образно говоря, линия на рисунке напоминает скалистый обрыв, а черные точки на графике напоминают камни, которые ранее упали вниз. Таким образом, внизу наблюдается как бы каменистая осыпь из таких точек. Справа от выбранной точки на оси абсцисс, лежит только "факторная осыпь". Согласно этому критерию, на приведенном рисунке, скорее всего, следует выбрать для воспроизведения двумерное пространство.

Интерпретируемость конфигурации.
Интерпретируемость конфигурации.

Вторым критерием для решения вопроса о размерности с целью интерпретации является "ясность" полученной конфигурации точек. Иногда, как в нашем примере с городами, результирующие координаты легко интерпретируются. В других случаях, точки на графике могут образовывать ту или иную разновидность "случайного облака", и не существует непосредственного способа для интерпретации латентных переменных.

В последнем случае следует постараться немного увеличить число координатных осей и рассмотреть получаемые в результате конфигурации. Чаще всего, получаемые решения проще удается проинтерпретировать. Однако если точки на графике не следуют какому-либо образцу, а также если график стресса не показывает какого-либо явного "изгиба" (и не похож на "край обрыва"), то данные скорее всего являются случайным "шумом".

В начало

Интерпретация осей координат

Интерпретация осей координат

Интерпретация осей обычно представляет собой заключительный этап анализа по методу многомерного шкалирования. Как уже упоминалось ранее, в принципе, ориентация осей в методе МНШ может быть произвольной, и систему координат можно повернуть в любом направлении. Поэтому на первом шаге получают диаграмму рассеяния точек, соответствующих объектам, на различных плоскостях.

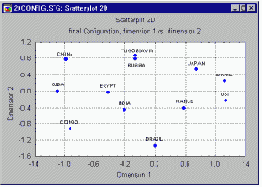
Трехмерные решения также можно проинтерпретировать графически.

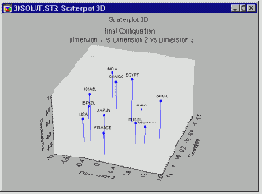
Однако эта интерпретация является несколько более сложной.
Заметим, что в дополнение к существенным осям координат, также следует искать кластеры точек, а также те или иные конфигурации точек (окружности, многообразия и др.). Более подробное обсуждение интерпретации полученных конфигураций, см. в работах Borg and Lingoes (1987), Borg and Shye (в печати) или Gutman, (1968).

Использование методов множественной регрессии.
Использование методов множественной регрессии.

Аналитическим способом интерпретации осей координат (описанным в работе Kruskal и Wish, 1978) является применение методов множественной регрессии для регрессирования некоторых имеющих смысл переменных на оси координат. Это легко сделать с помощью модуля Множественная регрессия.

В начало

Приложения

Приложения

"Красота" метода МНШ в том, что вы можете анализировать произвольный тип матрицы расстояний или сходства. Эти сходства могут представлять собой оценки экспертов относительно сходства данных объектов, результаты измерения расстояний в некоторой метрике, процент согласия между судьями по поводу принимаемого решения, количество раз, когда субъект затрудняется различить стимулы и мн.др.

Например, методы МНШ весьма популярны в психологическом исследовании восприятия личности. В этом исследовании анализируются сходства между определенными чертами характера с целью выявления основополагающими личностных качеств (см., например, Rosenberg, 1977). Также они популярны в маркетинговых исследованиях, где их используют для выявления числа и сущности латентных переменных (факторов), например, с целью с целью изучения отношения людей к товарам известных торговых марок (подробнее см. Green и Carmone, 1970).

В общем случае, методы МНШ позволяют исследователю задать клиентам в анкете относительно ненавязчивые вопросы ("насколько похож товар фирмы A на товар фирмы B") и найти латентные переменные для этих анкет незаметно для респондентов.

В начало

Многомерное шкалирование и факторный анализ

Многомерное шкалирование и факторный анализ

Даже несмотря на то, что имеется много сходства в характере исследуемых вопросов, методы МНШ и факторного анализа имеют ряд существенных отличий. Так, факторный анализ требует, чтобы исследуемые данные подчинялись многомерному нормальному распределению, а зависимости были линейными. Методы МНШ не накладывают таких ограничений. Методы МНШ могут быть применимы, пока сохраняет смысл порядок следования рангов сходств. В терминах различий получаемых результатов, факторный анализ стремится извлечь больше факторов (координатных осей или латентных переменных) по сравнению с МНШ; в результате чего МНШ часто приводит к проще интерпретируемым решениям. Однако более существенно то, что методы МНШ можно применять к любым типам расстояний или сходств, тогда как методы ФА требуют, чтобы первоначально была вычислена матрица корреляций. Методы МНШ могут быть основаны на прямом оценивании сходств между стимулами субъектов, тогда как ФА требует, чтобы субъекты были оценены через их стимулы по некоторому списку атрибутов.

Суммируя вышесказанное, можно сказать, что методы МНШ потенциально применимы к более широкому классу исследовательских задач.

В начало