Множественная регрессия

Множественная регрессия

Общее назначение
Вычислительные аспекты
- Метод наименьших квадратов
- Уравнение регрессии
- Однозначный прогноз и частная корреляция
- Предсказанные значения и остатки
- Остаточная дисперсия и коэффициент детерминации R-квадрат
- Интерпретация коэффициента множественной корреляции R
Предположения, ограничения и обсуждение практических вопросов
- Предположение линейности
- Предположение нормальности
- Ограничения
- Выбор числа переменных
- Мультиколлинеарность и плохая обусловленность матрицы
- Подгонка центрированных полиномиальных моделей
- Важность анализа остатков

Общее назначение

Общее назначение множественной регрессии (этот термин был впервые использован в работе Пирсона - Pearson, 1908) состоит в анализе связи между несколькими независимыми переменными (называемыми также регрессорами или предикторами) и зависимой переменной. Например, агент по продаже недвижимости мог бы вносить в каждый элемент реестра размер дома (в квадратных футах), число спален, средний доход населения в этом районе в соответствии с данными переписи и субъективную оценку привлекательности дома. Как только эта информация собрана для различных домов, было бы интересно посмотреть, связаны ли и каким образом эти характеристики дома с ценой, по которой он был продан. Например, могло бы оказаться, что число спальных комнат является лучшим предсказывающим фактором (предиктором) для цены продажи дома в некотором специфическом районе, чем "привлекательность" дома (субъективная оценка). Могли бы также обнаружиться и "выбросы", т.е. дома, которые могли бы быть проданы дороже, учитывая их расположение и характеристики.
Специалисты по кадрам обычно используют процедуры множественной регрессии для определения вознаграждения адекватного выполненной работе. Можно определить некоторое количество факторов или параметров, таких, как "размер ответственности" (Resp) или "число подчиненных" (No_Super), которые, как ожидается, оказывают влияние на стоимость работы.
Кадровый аналитик затем проводит исследование размеров окладов (Salary) среди сравнимых компаний на рынке, записывая размер жалования и соответствующие характеристики (т.е. значения параметров) по различным позициям. Эта информация может быть использована при анализе с помощью множественной регрессии для построения регрессионного уравнения в следующем виде:

Salary = .5*Resp + .8*No_Super

Как только эта так называемая линия регрессии определена, аналитик оказывается в состоянии построить график ожидаемой (предсказанной) оплаты труда и реальных обязательств компании по выплате жалования. Таким образом, аналитик может определить, какие позиции недооценены (лежат ниже линии регрессии), какие оплачиваются слишком высоко (лежат выше линии регрессии), а какие оплачены адекватно.

В общественных и естественных науках процедуры множественной регрессии чрезвычайно широко используются в исследованиях. В общем, множественная регрессия позволяет исследователю задать вопрос (и, вероятно, получить ответ) о том, "что является лучшим предиктором для...". Например, исследователь в области образования мог бы пожелать узнать, какие факторы являются лучшими предикторами успешной учебы в средней школе. А психолога мог быть заинтересовать вопрос, какие индивидуальные качества позволяют лучше предсказать степень социальной адаптации индивида. Социологи, вероятно, хотели бы найти те социальные индикаторы, которые лучше других предсказывают результат адаптации новой иммигрантской группы и степень ее слияния с обществом. Заметим, что термин "множественная" указывает на наличие нескольких предикторов или регрессоров, которые используются в модели.

В начало

Вычислительные аспекты
Вычислительные аспекты

Общая вычислительная задача, которую требуется решать при анализе методом множественной регрессии, состоит в подгонке прямой линии к некоторому набору точек.

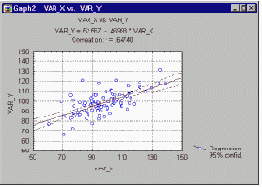
В простейшем случае, когда имеется одна зависимая и одна независимая переменная, это можно увидеть на диаграмме рассеяния.

Метод наименьших квадратов
Уравнение регрессии
Однозначный прогноз и частная корреляция
Предсказанные значения и остатки
Остаточная дисперсия и коэффициент детерминации R-квадрат
Интерпретация коэффициента множественной корреляции R

Метод наименьших квадратов.
Метод наименьших квадратов.

На диаграмме рассеяния имеется независимая переменная или переменная X и зависимая переменная Y. Эти переменные могут, например, представлять коэффициент IQ (уровень интеллекта, оцененный с помощью теста) и достижения в учебе (средний балл успеваемости - grade point average; GPA) соответственно. Каждая точка на диаграмме представляет данные одного студента, т.е. его соответствующие показатели IQ и GPA. Целью процедур линейной регрессии является подгонка прямой линии по точкам. А именно, программа строит линию регрессии так, чтобы минимизировать квадраты отклонений этой линии от наблюдаемых точек. Поэтому на эту общую процедуру иногда ссылаются как на оценивание по методу наименьших квадратов. (см. также описание оценивания по методу взвешенных наименьших квадратов). Уравнение регрессии.
Уравнение регрессии.

Прямая линия на плоскости (в пространстве двух измерений) задается уравнением Y=a+b*X; более подробно: переменная Y может быть выражена через константу (a) и угловой коэффициент (b), умноженный на переменную X. Константу иногда называют также свободным членом, а угловой коэффициент - регрессионным или B-коэффициентом. Например, значение GPA можно лучше всего предсказать по формуле 1+.02*IQ. Таким образом, зная, что коэффициент IQ у студента равен 130, вы могли бы предсказать его показатель успеваемости GPA, скорее всего, он близок к 3.6 (поскольку 1+.02*130=3.6). Например, анимационный ролик ниже показывает доверительные интервалы (90%, 95% и 99%), построенные для двумерного регрессионного уравнения.

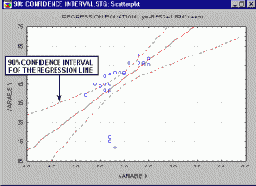
В многомерном случае, когда имеется более одной независимой переменной, линия регрессии не может быть отображена в двумерном пространстве, однако она также может быть легко оценена. Например, если в дополнение к IQ вы имеете другие предикторы успеваемости (например, Мотивация, Самодисциплина), вы можете построить линейное уравнение, содержащее все эти переменные. Тогда, в общем случае, процедуры множественной регрессии будут оценивать параметры линейного уравнения вида:

Y = a + b1*X1 + b2*X2 + ... + bp*Xp

Однозначный прогноз и частная корреляция.
Однозначный прогноз и частная корреляция.

Регрессионные коэффициенты (или B-коэффициенты) представляют независимые вклады каждой независимой переменной в предсказание зависимой переменной. Другими словами, переменная X1, к примеру, коррелирует с переменной Y после учета влияния всех других независимых переменных. Этот тип корреляции упоминается также под названием частной корреляции (этот термин был впервые использован в работе Yule, 1907). Вероятно, следующий пример пояснит это понятие. Кто-то мог бы, вероятно, обнаружить значимую отрицательную корреляцию в популяции между длиной волос и ростом (невысокие люди обладают более длинными волосами). На первый взгляд это может показаться странным; однако, если добавить переменную Пол в уравнение множественной регрессии, эта корреляция, скорее всего, исчезнет. Это произойдет из-за того, что женщины, в среднем, имеют более длинные волосы, чем мужчины; при этом они также в среднем ниже мужчин. Таким образом, после удаления разницы по полу посредством ввода предиктора Пол в уравнение, связь между длиной волос и ростом исчезает, поскольку длина волос не дает какого-либо самостоятельного вклада в предсказание роста помимо того, который она разделяет с переменной Пол. Другими словами, после учета переменной Пол частная корреляция между длиной волос и ростом нулевая. Иными словами, если одна величина коррелирована с другой, то это может быть отражением того факта, что они обе коррелированы с третьей величиной или с совокупностью величин. Предсказанные значения и остатки.
Предсказанные значения и остатки.

Линия регрессии выражает наилучшее предсказание зависимой переменной (Y) по независимым переменным (X). Однако, природа редко (если вообще когда-нибудь) бывает полностью предсказуемой и обычно имеется существенный разброс наблюдаемых точек относительно подогнанной прямой (как это было показано ранее на диаграмме рассеяния). Отклонение отдельной точки от линии регрессии (от предсказанного значения) называется остатком. Остаточная дисперсия и коэффициент детерминации R-квадрат.

Остаточная дисперсия и коэффициент детерминации R-квадрат.

Чем меньше разброс значений остатков около линии регрессии по отношению к общему разбросу значений, тем, очевидно, лучше прогноз. Например, если связь между переменными X и Y отсутствует, то отношение остаточной изменчивости переменной Y к исходной дисперсии равно 1.0. Если X и Y жестко связаны, то остаточная изменчивость отсутствует, и отношение дисперсий будет равно 0.0. В большинстве случаев отношение будет лежать где-то между этими экстремальными значениями, т.е. между 0.0 и 1.0. 1.0 минус это отношение называется R-квадратом или коэффициентом детерминации. Это значение непосредственно интерпретируется следующим образом. Если имеется R-квадрат равный 0.4, то изменчивость значений переменной Y около линии регрессии составляет 1-0.4 от исходной дисперсии; другими словами, 40% от исходной изменчивости могут быть объяснены, а 60% остаточной изменчивости остаются необъясненными. В идеале желательно иметь объяснение если не для всей, то хотя бы для большей части исходной изменчивости. Значение R-квадрата является индикатором степени подгонки модели к данным (значение R-квадрата близкое к 1.0 показывает, что модель объясняет почти всю изменчивость соответствующих переменных). Интерпретация коэффициента множественной корреляции R.
Интерпретация коэффициента множественной корреляции R.

Обычно, степень зависимости двух или более предикторов (независимых переменных или переменных X) с зависимой переменной (Y) выражается с помощью коэффициента множественной корреляции R. По определению он равен корню квадратному из коэффициента детерминации. Это неотрицательная величина, принимающая значения между 0 и 1. Для интерпретации направления связи между переменными смотрят на знаки (плюс или минус) регрессионных коэффициентов или B-коэффициентов. Если B-коэффициент положителен, то связь этой переменной с зависимой переменной положительна (например, чем больше IQ, тем выше средний показатель успеваемости оценки); если B-коэффициент отрицателен, то и связь носит отрицательный характер (например, чем меньше число учащихся в классе, тем выше средние оценки по тестам).

Конечно, если B- коэффициент равен 0, связь между переменными отсутствует.

В начало

Предположения, ограничения и обсуждение практических вопросов
Предположения, ограничения и обсуждение практических вопросов

Предположение линейности
Предположение нормальности
Ограничения
Выбор числа переменных
Мультиколлинеарность и плохая обусловленность матрицы
Важность анализа остатков

Предположение линейности
Предположение нормальности
Ограничения
Выбор числа переменных
Мультиколлинеарность и плохая обусловленность матрицы
Важность анализа остатков

Предположение линейности.
Предположение линейности.

Прежде всего, как это видно уже из названия множественной линейной регрессии, предполагается, что связь между переменными является линейной. На практике это предположение, в сущности, никогда не может быть подтверждено; к счастью, процедуры множественного регрессионного анализы в незначительной степени подвержены воздействию малых отклонений от этого предположения. Однако всегда имеет смысл посмотреть на двумерные диаграммы рассеяния переменных, представляющих интерес. Если нелинейность связи очевидна, то можно рассмотреть или преобразования переменных или явно допустить включение нелинейных членов.

Предположение нормальности.
Предположение нормальности.

В множественной регрессии предполагается, что остатки (предсказанные значения минус наблюдаемые) распределены нормально (т.е. подчиняются закону нормального распределения). И снова, хотя большинство тестов (в особенности F-тест) довольно робастны (устойчивы) по отношению к отклонениям от этого предположения, всегда, прежде чем сделать окончательные выводы, стоит рассмотреть распределения представляющих интерес переменных. Вы можете построить гистограммы или нормальные вероятностные графики остатков для визуального анализа их распределения. Ограничения.
Ограничения.

Основное концептуальное ограничение всех методов регрессионного анализа состоит в том, что они позволяют обнаружить только числовые зависимости, а не лежащие в их основе причинные (causal) связи.

Например, можно обнаружить сильную положительную связь (корреляцию) между разрушениями, вызванными пожаром, и числом пожарных, участвующих в борьбе с огнем. Следует ли заключить, что пожарные вызывают разрушения? Конечно, наиболее вероятное объяснение этой корреляции состоит в том, что размер пожара (внешняя переменная, которую забыли включить в исследование) оказывает влияние, как на масштаб разрушений, так и на привлечение определенного числа пожарных (т.е. чем больше пожар, тем большее количество пожарных вызывается на его тушение). Хотя этот пример довольно прозрачен, в реальности при исследовании корреляций альтернативные причинные объяснения часто даже не рассматриваются. Выбор числа переменных.
Выбор числа переменных.

Множественная регрессия - предоставляет пользователю "соблазн" включить в качестве предикторов все переменные, какие только можно, в надежде, что некоторые из них окажутся значимыми. Это происходит из-за того, что извлекается выгода из случайностей, возникающих при простом включении возможно большего числа переменных, рассматриваемых в качестве предикторов другой, представляющей интерес переменной. Эта проблема возникает тогда, когда к тому же и число наблюдений относительно мало. Интуитивно ясно, что едва ли можно делать выводы из анализа вопросника со 100 пунктами на основе ответов 10 респондентов. Большинство авторов советуют использовать, по крайней мере, от 10 до 20 наблюдений (респондентов) на одну переменную, в противном случае оценки регрессионной линии будут, вероятно, очень ненадежными и, скорее всего, невоспроизводимыми для желающих повторить это исследование. Мультиколлинеарность и плохая обусловленность матрицы.
Мультиколлинеарность и плохая обусловленность матрицы.

Проблема мультиколлинеарности является общей для многих методов корреляционного анализа. Представим, что имеется два предиктора (переменные X) для роста субъекта: (1) вес в фунтах и (2) вес в унциях. Очевидно, что иметь оба предиктора совершенно излишне; вес является одной и той же переменной, измеряется он в фунтах или унциях.

Попытка определить, какая из двух мер является лучшим предиктором, выглядит довольно глупо; однако, в точности это происходит при попытке выполнить множественный регрессионный анализ с ростом в качестве зависимой переменной (Y) и двумя мерами веса, как независимыми переменными (X). Если в анализ включено много переменных, то часто не сразу очевидно существование этой проблемы, и она может возникнуть только после того, как некоторые переменные будут уже включены в регрессионное уравнение. Тем не менее, если такая проблема возникает, это означает, что, по крайней мере, одна из зависимых переменных (предикторов) является совершенно лишней при наличии остальных предикторов. Существует довольно много статистических индикаторов избыточности (толерантность, получастное R и др.), а также немало средств для борьбы с избыточностью (например, метод Гребневая регрессия). Подгонка центрированных полиномиальных моделей.
Подгонка центрированных полиномиальных моделей.

Подгонка полиномов высших порядков от независимых переменных с ненулевым средним может создать большие трудности с мультиколлинеарностью. А именно, получаемые полиномы будут сильно коррелированы из-за этого среднего значения первичной независимой переменной. При использовании больших чисел (например, дат в Юлианском исчислении), Эта проблема становится очень серьезной, и если не принять соответствующих мер, то можно прийти к неверным результатам. Решением в данном случае является процедура центрирования независимой переменной, т.е. вначале вычесть из переменной среднее, а затем вычислять многочлены. Более подробное обсуждение этого вопроса (и анализа полиномиальных моделей в целом) смотрите, например, в классической работе Neter, Wasserman & Kutner (1985, глава 9). Важность анализа остатков.
Важность анализа остатков.

Хотя большинство предположений множественной регрессии нельзя в точности проверить, исследователь может обнаружить отклонения от этих предположений. В частности, выбросы (т.е. экстремальные наблюдения) могут вызвать серьезное смещение оценок, "сдвигая" линию регрессии в определенном направлении и тем самым, вызывая смещение регрессионных коэффициентов.Часто исключение всего одного экстремального наблюдения приводит к совершенно другому результату.

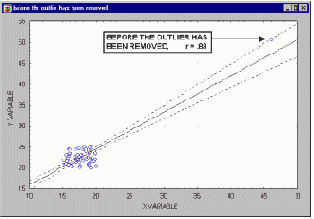
В начало