Нелинейное оценивание

Нелинейное оценивание

Общее назначение
Оценивание линейных и нелинейных моделей
Основные типы нелинейных моделей
- Регрессионные модели с линейной структурой
- Существенно нелинейные регрессионные модели
Методы нелинейного оценивания
- Метод наименьших квадратов
- Функция потерь
- Метод взвешенных наименьших квадратов
- Метод максимума правдоподобия
- Максимум правдоподобия и логит/пробит модели
- Алгоритмы минимизации функций
- Начальные значения, размеры шагов и критерий сходимости
- Штрафные функции, ограничение параметров
- Локальные минимумы
- Квази-ньютоновский метод
- Симплекс-метод
- Метод Хука-Дживиса
- Метод Розенброка
- Матрица Гессе и стандартные ошибки
Оценивание пригодности модели
- Объясненная доля дисперсии
- Критерий согласия хи-квадрат
- График наблюдаемых и предсказанных значений
- Нормальный и полунормальный график остатков
- График функции подгонки
- Ковариационная матрица оценок параметров

Общее назначение
Оценивание линейных и нелинейных моделей
Основные типы нелинейных моделей
- Регрессионные модели с линейной структурой
- Существенно нелинейные регрессионные модели
Методы нелинейного оценивания
- Метод наименьших квадратов
- Функция потерь
- Метод взвешенных наименьших квадратов
- Метод максимума правдоподобия
- Максимум правдоподобия и логит/пробит модели
- Алгоритмы минимизации функций
- Начальные значения, размеры шагов и критерий сходимости
- Штрафные функции, ограничение параметров
- Локальные минимумы
- Квази-ньютоновский метод
- Симплекс-метод
- Метод Хука-Дживиса
- Метод Розенброка
- Матрица Гессе и стандартные ошибки
Оценивание пригодности модели
- Объясненная доля дисперсии
- Критерий согласия хи-квадрат
- График наблюдаемых и предсказанных значений
- Нормальный и полунормальный график остатков
- График функции подгонки
- Ковариационная матрица оценок параметров

Общее назначение
Общее назначение

Иногда, при проведении анализа линейной модели, исследователь получает данные о ее неадекватности. В этом случае, его по-прежнему интересует зависимость между предикторными переменными и откликом, но для уточнения модели в ее уравнение добавляются некоторые нелинейные члены.
Самым удобным способом оценивания параметров полученной регрессии является Нелинейное оценивание. Например, его можно использовать для уточнения зависимости между дозой и эффективностью лекарства, стажем работы и производительностью труда, стоимостью дома и временем, необходимым для его продажи и т.д. Наверное, вы заметили, что ситуации, рассматриваемые в этих примерах, часто интересовали нас и в таких методах как множественная регрессия (см. Множественная регрессия) и дисперсионный анализ (см. Дисперсионный анализ). На самом деле, можно считать Нелинейное оценивание обобщением этих двух методов. Так, в методе множественной регрессии (и в дисперсионном анализе) предполагается, что зависимость отклика от предикторных переменных линейна. Нелинейное оценивание оставляет выбор характера зависимости за вами. Например, вы можете определить зависимую переменную как логарифмическую функцию от предикторной переменной, как степенную функцию, или как любую другую композицию элементарных функций от предикторов (однако, если все изучаемые переменные категориальны по своей природе, вы можете также воспользоваться модулем Анализ соответствий).

Если позволить рассмотрение любого типа зависимости между предикторами и переменной отклика, возникают два вопроса. Во-первых, как истолковать найденную зависимость в виде простых практических рекомендаций. С этой точки зрения линейная зависимость очень удобна, так как позволяет дать простое пояснение: “чем больше x (т.е., чем больше цена дома), тем больше y (тем больше времени нужно, чтобы его продать); и, задавая конкретные приращения x, можно ожидать пропорциональное приращение y”. Нелинейные соотношения обычно нельзя так просто проинтерпретировать и выразить словами. Второй вопрос - как проверить, имеется ли на самом деле предсказанная нелинейная зависимость.

Далее мы рассмотрим проблему нелинейной регрессии более формально и введем стандартную терминологию, позволяющую рассмотреть сущность этого метода более пристально. Мы также покажем примеры его использования в различных областях исследований: медицине, социологии, физике, химии, фармакологии, проектировании и т.д.

В начало

Оценивание линейных и нелинейных моделей
Оценивание линейных и нелинейных моделей

Формально говоря, модуль Нелинейное оценивание является универсальной аппроксимирующей процедурой, оценивающей любой вид зависимости между переменной отклика и набором независимых переменных. В общем случае, все регрессионные модели могут быть записаны в виде формулы:

y = F(x1, x2, ... , xn)

При проведении регрессионного, а в частности нелинейного регрессионного анализа, исследователя интересует, связана ли и если да, то как, зависимая переменная и набор независимых переменных. Выражение F(x...) в выписанном выше выражении означает, что переменная отклика y является функцией от независимой переменной x.

Примером модели такого типа может быть модель множественной линейной регрессии, описанная в разделе Множественная регрессия. В этой модели предполагается, что зависимая переменная является линейной функцией независимых переменных, т.е.:

y = a + b1*x1 + b2*x2 + ... + bn*xn

Если вы не знакомы с множественной линейной регрессией, вы можете прямо сейчас перечитать вводный обзор Множественной регрессии (но вам вовсе не обязательно понимать все нюансы множественной линейной регрессии, для того чтобы разобраться в обсуждаемом здесь методе).

Нелинейное оценивание позволяет задать практически любой тип непрерывной или разрывной регрессионной модели. Некоторые из наиболее общих нелинейных моделей (такие как пробит и логит модели, модель экспоненциального роста и регрессия с точками разрыва) уже имеются в Нелинейном оценивании. Однако, при необходимости, вы можете также самостоятельно ввести регрессионное уравнение любого типа, поручив программе его подгонку в соответствии с вашими данными. Более того, для оценивания модели вы можете использовать метод наименьших квадратов, метод максимума правдоподобия (если это допускается выбранной моделью), или, опять же, определить вашу собственную функцию потерь (см. ниже) задав соответствующее уравнение.

В общем случае, каждый раз, когда простая модель линейной регрессии неадекватно отражает зависимость переменных, используется модель нелинейной регрессии.

Выберите один из следующих разделов для получения более полного представления об основных типах нелинейных моделей, процедурах нелинейного оценивания и оценивании пригодности модели.

Основные типы нелинейных моделей

Регрессионные модели с линейной структурой
Существенно нелинейные регрессионные модели

Основные типы нелинейных моделей

Регрессионные модели с линейной структурой
Существенно нелинейные регрессионные модели

Регрессионные модели с линейной структурой Полиномиальная регрессия.
Полиномиальная регрессия.

Распространенной “нелинейной” моделью является модель полиномиальной регрессии. Термин нелинейная заключен в кавычки, поскольку эта модель линейна по своей природе. Например, предположим, что вы измеряете в обучающем эксперименте связь физиологического возбуждения объектов и их производительности в задаче слежения за целями. На основании хорошо известного закона Йеркса-Додсона, можно ожидать нелинейной зависимости между уровнем возбуждения и производительностью. Это предположение можно выразить следующим уравнением регрессии:

Производительность = a + b1*Возбуждение + b2*Возбуждение2

В этом уравнении, a представляет свободный член, а b1 и b2 коэффициенты регрессии. Нелинейность этой модели выражается членом Возбуждение2. Однако, в сущности, модель по-прежнему линейна, за исключением того, что при ее оценивании нам придется возводить наблюдаемый уровень возбуждения в квадрат. Для оценивания коэффициентов регрессии этой модели можно использовать фиксированное нелинейное оценивание. Такие модели, где мы составляем линейное уравнение из некоторых преобразований независимых переменных, относятся к моделям нелинейным по переменным.

Модели, нелинейные по параметрам.
Модели, нелинейные по параметрам.

Для сравнения с предыдущим примером рассмотрим зависимость между возрастом человека (переменная x) и его скоростью роста (переменная y). Очевидно, что соотношение между этими двумя переменными на первом году человеческой жизни (когда происходит наибольший рост) сильно отличается от соотношения во взрослом возрасте (когда человек почти не растет).

Поэтому, эту зависимость лучше представить в виде какой-нибудь экспоненциальной функции с отрицательным показателем степени:

Рост = exp(-b1*Возраст)

Если вы построите на графике оценку для коэффициента регрессии, то вы получите кривую следующего вида:

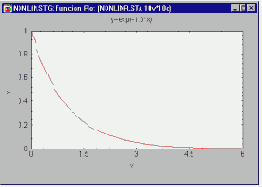
Отметим, что эта модель по своей природе больше не является линейной, т.е. выражение, написанное сверху, не представимо в виде простой регрессионной модели с некоторыми преобразованиями независимых переменных. Такие модели называются нелинейными по параметрам.

Сведение нелинейных моделей к линейным.
Сведение нелинейных моделей к линейным.

В общем случае, всегда, когда регрессионная модель может быть сведена к линейной модели, этому способу отдается предпочтение (при оценивании соответствующей модели). Модель линейной множественной регрессии (см. Множественная регрессия) наиболее просто понимаема с точки зрения математики и, с практической точки зрения, наиболее проста для толкования. Поэтому, возвращаясь к простой экспоненциальной регрессионной модели Скорости роста как функции Возраста, описанной раньше, мы можем преобразовать это нелинейное уравнение в линейное, прологарифмировав обе части уравнения, получив:

log(Рост) = -b1*Возраст

Если теперь заменить log(Рост)) на y, мы получим стандартную модель линейной регрессии, как уже было показано раньше (без свободного члена, который был опущен для простоты изложения). Таким образом, для оценивания взаимоотношения возраста и скорости роста вы можете прологарифмировать данные о скорости роста (например, воспользовавшись преобразованиями таблиц данных с помощью формул), а затем использовать Множественную регрессию, получив при этом интересующий нас коэффициент регрессии b1.

Адекватность модели.
Адекватность модели.

Конечно, используя “неправильное” преобразование, можно прийти к неадекватной модели. Поэтому, после ”линеаризации” модели, наподобие только что показанной, очень важно провести подробное изучение статистик остатков, вычисляемых с помощью Множественной регрессии.

Существенно нелинейные регрессионные модели

Для некоторых регрессионных моделей, которые не могут быть сведены к линейным, единственным способом для исследования остается Нелинейное оценивание. В приведенном выше примере для скорости роста, мы специально “забыли ” о случайной ошибке в зависимой переменной. Конечно, на скорость роста влияют множество других факторов (кроме возраста), и нам следует ожидать значительных случайных отклонений (остатков) от предложенной нами кривой. Если добавить эту ошибку или остаточную изменчивость, нашу модель можно переписать следующим образом:

Рост = exp(-b1*Возраст) + ошибка

Аддитивная ошибка.
Аддитивная ошибка.

В этой модели предполагается, что случайная ошибка не зависит от возраста, т.е., остаточная изменчивость одинакова для всех возрастов. Поскольку ошибка в этой модели аддитивна, т.е. просто прибавляется к точному значению скорости роста, мы больше не можем линеаризовать эту модель простым логарифмированием обеих частей. Если бы мы снова прологарифмировали входные данные о скорости роста и подобрали простую линейную модель, мы заметили бы, что остатки больше не являются равномерно распределенными вокруг значений переменной возраст; и поэтому, стандартный линейный регрессионный анализ (с помощью Множественной регрессии) больше не применим. Единственным способом оценивания параметров модели остается использование Нелинейного оценивания.

Мультипликативная ошибка.
Мультипликативная ошибка.

В “оправдание” предыдущего примера заметим, что в данном случае постоянство вариации случайной ошибки в любом возрасте мало вероятно, т.е., предположение об аддитивности ошибки не слишком реалистично. Правдоподобнее, что изменения скорости роста более случайны и непредсказуемы в раннем возрасте, чем в позднем, когда рост практически останавливается. Поэтому, более реалистичной моделью, включающей ошибку, будет:

Рост = exp(-b1*Возраст) * ошибка

На словах это означает, что чем больше возраст, тем меньше множитель exp(-b1*Возраст), и, следовательно, тем меньше будет разброс результирующей ошибки.

Если же вы теперь прологарифмируете обе части нашего уравнения, то остаточная ошибка перейдет в свободный член линейного уравнения, т.е., аддитивный фактор, и вы сможете продолжить и оценить b1 пользуясь стандартную множественную регрессию.

Log (Рост) = -b1*Возраст + ошибка

Теперь мы рассмотрим некоторые регрессионные модели (нелинейные по параметрам), которые не могут быть сведены к линейным простым преобразованием начальных данных.

Общая модель роста.
Общая модель роста.

Общая модель роста похожа на рассмотренный ранее пример:

y = b0 + b1*exp(b2*x) + ошибка

Эта модель обычно используется при изучении различных видов роста (y), когда скорость роста в любой момент времени (x) пропорциональна оставшемуся приросту. Параметр b0 в этой модели представляет максимальное значение скорости роста. Типичным примером ее адекватного использования служит описание концентрации вещества (например, в воде) в виде функции времени.

Модели бинарных откликов: пробит и логит.
Модели бинарных откликов: пробит и логит.

Нередко зависимая переменная - переменная отклика бинарна по своей природе, т.е. может принимать только два значения. Например, пациент может выздороветь, а может и нет, кандидат на должность может пройти, а может провалить тест при приеме на работу, подписчики журнала могут продлить, а могут не продлевать подписку, купоны скидок могут быть использованы, а могут быть и не использованы и т.п. Во всех этих случаях нас может заинтересовать поиск зависимости между одной или несколькими “непрерывными” переменными и одной, зависящей от них бинарной переменной.

Использование линейной регрессии. Конечно, можно использовать стандартную множественную регрессию и вычислить стандартные коэффициенты регрессии. Например, если рассматривается продление журнальной подписки, можно задать переменную y со значениями 1’ и 0’, где 1 означает, что соответствующий подписчик продлил подписку, а 0, что он отказался от продления. Однако здесь возникает проблема: Множественная регрессия не “знает”, что переменная отклика бинарна по своей природе.

Поэтому, это неизбежно приведет к модели с предсказываемыми значениями большими 1 и меньшими 0. Но такие значения вообще не допустимы для первоначальной задачи, таким образом, множественная регрессия просто игнорирует ограничения на диапазон значений для y.

Непрерывные функции отклика. Задача регрессии может быть сформулирована иначе: вместо предсказания бинарной переменной, мы предсказываем непрерывную переменную со значениями на отрезке [0,1]. Наибольшее распространение в этой области получили регрессионные модели логит и пробит.

Логит регрессия. В этой модели предсказываемые значения для зависимой переменной больше или равны 0 и меньше или равны 1 при любых значениях независимых переменных. Это достигается применением следующего регрессионного уравнения, которое в действительности имеет также некоторый глубокий смысл, как вы вскоре увидите (термин логит впервые был использован в работе Berkson, 1944):

y = exp(b0 + b1*x1 + ... + bn*xn)/{1 + exp(b0 + b1*x1 + ... + bn*xn)}

Легко заметить, что вне зависимости от коэффициентов регрессии и значений x, значения y, предсказанные этой моделью всегда будут принадлежать отрезку [0,1].

Название логит этой модели происходит от названия простого способа сведения этой модели к линейной с помощью логит преобразования. Предположим, что мы рассуждаем о нашей зависимой переменной в терминах нашей основной вероятности p, лежащей между 0 и 1. Тогда мы можем преобразовать эту вероятность p:

p' = loge{p/(1-p)}

Это преобразование обычно называют логистическим или логит - преобразованием. Отметим, что теоретически p’ может принимать любое значение от минус до плюс бесконечности. Поскольку логистическое преобразование решает проблему об ограничении на 0-1 границы для первоначальной зависимой переменной (вероятности), вы можете использовать эти (преобразованные) значения в обычном линейном регрессионном уравнении. А именно, если произвести логистическое преобразование обеих частей описанного выше уравнения, мы получим стандартную модель линейной регрессии:

p' = b0 + b1*x1 + b2*x2 + ... + bn*xn

Пробит регрессия.
Пробит регрессия.

Можно рассматривать бинарную зависимую переменную как отклик на изменения некоторой “основной”, нормально распределенной переменной, в действительности имеющую диапазон изменений от минус до плюс бесконечности. Например, подписчик журнала может быть решительно против продления подписки, находится в нерешительности или испытывать расположение к журналу и стремиться продлить подписку. В любом случае, все, что мы (как издатели журнала) увидим, будет бинарный отклик, означающий продление или отказ от продления подписки. Однако если мы запишем стандартное уравнение линейной регрессии, основанное на “отношении людей к журналу”, мы получим:

отношение... = b0 + b1*x1 + ...

что, конечно, соответствует стандартной регрессионной модели. Логично предположить, что это “отношение людей к журналу” нормально распределено, и что вероятность продления подписки p равна соответствующей “отношению к журналу ” площади под графиком плотности нормального распределения. Поэтому, если мы преобразуем обе части уравнения в соответствующие нормальные вероятности, мы получим:

NP(отношение...) = NP(b0 + b1*x1 + ...)

Здесь NP означает нормальную вероятность (площадь под графиком плотности нормального распределения), таблицы которой имеются практически в любом статистическом справочнике. Выписанное выше уравнение называется также регрессионной моделью пробит. (Термит пробит был впервые использован в работе Bliss, 1934.)

Обобщенная логит регрессия.
Обобщенная логит регрессия.

Обобщенная логит регрессия может быть выражена уравнением:

y = b0/{1 + b1*exp(b2*x)}

Вы можете представлять себе эту модель как обобщение обычной логит модели для бинарных зависимых переменных. Однако если логит модель ограничивает значения зависимой переменной только двумя возможными значениями, то общая модель позволяет отклику произвольно меняться внутри фиксированного интервала. Например, предположим, что вас интересует прирост популяции вида, перенесенного на новое место обитания, рассмотренный в виде функции времени.

Тогда зависимая переменная будет равна числу особей данного вида в соответствующей среде обитания. Очевидно, что ее значение ограничено снизу, так как число особей не может быть меньше нуля; вероятно, что также существует какой-то верхний предел для численности популяции, который будет достигнут в некоторый момент времени.

Восприимчивость к лекарству и полумаксимальный отклик
Восприимчивость к лекарству и полумаксимальный отклик

. В фармакологии, для описания эффективности различных доз лекарственных средств, часто используется следующая модель:

y = b0 - b0/{1 + (x/b2)b1}

В этой модели, x означает размер дозы (обычно в некоторой закодированной форме, так что x

1), а y соответствует восприимчивости, измеренной в процентах по отношению к максимально возможной. Параметр b0 тогда означает ожидаемый отклик при насыщающем уровне дозы, а b2 равен концентрации, вызывающей полумаксимальный отклик; параметр b1 определяет наклон графика предсказываемой функции.

Регрессионные модели сточками разрыва
Кусочно - линейная регрессия.
Регрессионные модели сточками разрыва
Кусочно - линейная регрессия.

Нередко вид зависимости между предикторами и переменной отклика различается в разных областях значений независимых переменных. Например, вы рассматриваете себестоимость единицы некоторого продукта как функцию от объема произведенной продукции за месяц. Обычно, чем больше единиц товара вы производите, тем ниже себестоимость каждой единицы, и эта линейная зависимость существует в широких пределах изменения объема произведенной продукции. Однако при прохождении кривой выпуска через некоторые значения себестоимость может меняться скачкообразно. Например, себестоимость может увеличиваться при увеличении объема производства из-за того, что для производства дополнительных единиц используются другие (устаревшие) станки. Допустим, что устаревшие машины используются в производстве при достижении объемом производства уровня 500 единиц в месяц; этой ситуации соответствует следующая регрессионную модель для себестоимости:

y = b0 + b1*x*(x

500) + b2*x*(x > 500)

В этой формуле: y означает оцениваемую себестоимость, а x равен объему продукции, произведенной за месяц. Выражения (x

500) и (x > 500) обозначают логические условия, принимающие значения 1 если они истинны, и 0 иначе. Таким образом, эта модель определяется общим свободным членом (b0) и угловым коэффициентом, соответствующим b1 (если выражение x

500 истинно, т.е., равно 1) или b2 (если выражение x > 500 истинно, т.е., равно 1).

Вместо явного задания точки разрыва регрессионной кривой (500 единиц в месяц в последнем примере), можно также оценить положение этой точки. Например, мы могли заметить и предположить, что кривая себестоимости имеет разрыв в некоторой точке; однако не всегда очевидно, в какой именно точке происходит разрыв. В этом случае, достаточно просто заменить 500 в выписанном выше уравнении на дополнительный параметр (например, b3).

Регрессия с точками разрыва. Выписанное выше уравнение можно легко преобразовать к регрессии с точками разрыва, т.е. добавить скачкообразные изменения в некоторых точках кривой. Например, предположим, что после запуска устаревших станков, себестоимость “подпрыгнула” до более высокого уровня и затем продолжила медленно уменьшаться при увеличении объема производства. В этом случае, достаточно просто добавить (b3), тогда:

y = (b0 + b1*x)*(x

500) + (b3 + b2*x)*(x > 500)

Сравнение групп. Описанный здесь метод для оценивания различных регрессионных уравнений в разных областях значений независимых переменных может также быть использован для распознавания принадлежности элементов различным группам. Например, пусть в рассмотренном выше примере имеется три различных завода. Для простоты изложения “забудем” пока про возможные точки разрыва. Если сгруппировать переменные по принадлежности к соответствующему заводу, присвоив группирующей переменной значения 1,2 и 3, соответственно, мы сможем одновременно записать три различных регрессионных уравнения:

y = (xp=1)*(b10 + b11*x) + (xp=2)*(b20 + b21*x) + (xp=3)*(b30 + b31*x)

В этом уравнении, xp обозначает группирующую переменную, содержащую коды, определяющие завод, b10, b20 и b30 соответствуют свободным членам, а b11, b21 и b31 определяют угловые коэффициенты графика себестоимости (коэффициенты регрессии) для каждого завода. Вы можете сравнить правдоподобие этой и обычной регрессионной модели (без рассмотрения различных заводов) для того, чтобы определить более подходящую.

В начало

Методы нелинейного оценивания

Метод наименьших квадратов
Функция потерь
Метод взвешенных наименьших квадратов
Метод максимума правдоподобия
Максимум правдоподобия и логит/пробит модели
Алгоритмы минимизации функций
Начальные значения, размеры шагов и критерий сходимости
Штрафные функции, ограничение параметров
Локальные минимумы
Квази-ньютоновский метод
Симплекс-метод
Метод Хука-Дживиса
Метод Розенброка
Матрица Гессе и стандартные ошибки

Методы нелинейного оценивания

Метод наименьших квадратов
Функция потерь
Метод взвешенных наименьших квадратов
Метод максимума правдоподобия
Максимум правдоподобия и логит/пробит модели
Алгоритмы минимизации функций
Начальные значения, размеры шагов и критерий сходимости
Штрафные функции, ограничение параметров
Локальные минимумы
Квази-ньютоновский метод
Симплекс-метод
Метод Хука-Дживиса
Метод Розенброка
Матрица Гессе и стандартные ошибки

Метод наименьших квадратов.
Метод наименьших квадратов.

Некоторые более общие типы регрессионных моделей рассмотрены в разделе Основные типы нелинейных моделей. После выбора модели возникает вопрос: каким образом можно оценить эти модели? Если вы знакомы с методами линейной регрессии (описанными в разделе Множественная регрессия) или дисперсионного анализа (описанными в разделе Дисперсионный анализ), то вы знаете, что все эти методы используют оценивание по методу наименьших квадратов. Основной смысл этого метода заключается в минимизации суммы квадратов отклонений наблюдаемых значений зависимой переменной от значений, предсказанных моделью. (Термин наименьшие квадраты впервые был использован в работе Лежандра - Legendre, 1805.)

Функция потерь.

Функция потерь.

В стандартной множественной регрессии оценивание коэффициентов регрессии происходит “подбором” коэффициентов, минимизирующих дисперсию остатков (сумму квадратов остатков). Любые отклонения наблюдаемых величин от предсказанных означают некоторые потери в точности предсказаний, например, из-за случайного шума (ошибок). Поэтому можно сказать, что цель метода наименьших квадратов заключается в минимизации функции потерь. В этом случае, функция потерь определяется как сумма квадратов отклонений от предсказанных значений (термин функция потерь был впервые использован в работе Вальда - Wald, 1939). Когда эта функция достигает минимума, вы получаете те же оценки для параметров (свободного члена, коэффициентов регрессии), как, если бы мы использовали Множественную регрессию. Полученные оценки называются оценками по методу наименьших квадратов. Продолжая в том же духе, можно рассмотреть другие функции потерь. Например, при минимизации функции потерь, почему бы вместо суммы квадратов отклонений не рассмотреть сумму модулей отклонений? В самом деле, иногда это бывает полезно для уменьшения влияния выбросов. Влияние, оказываемое крупными остатками на всю сумму, существенно увеличивается при их возведении в квадрат. Однако если вместо суммы квадратов взять сумму модулей выбросов, влияние остатков на результирующую регрессионную кривую существенно уменьшится. Существуют несколько методов, которые могут быть использованы для минимизации различных видов функций потерь. Для получения дополнительной информации смотрите:

Метод наименьших квадратов
Функция потерь
Метод взвешенных наименьших квадратов
Метод максимума правдоподобия
Максимум правдоподобия и логит/пробит модели
Алгоритмы минимизации функций
Начальные значения, размеры шагов и критерий сходимости
Штрафные функции, ограничение параметров
Локальные минимумы
Квази-ньютоновский метод
Симплекс-метод
Метод Хука-Дживиса
Метод Розенброка
Матрица Гессе и стандартные ошибки

Метод взвешенных наименьших квадратов.

Метод взвешенных наименьших квадратов.

Третьим по распространенности методом, в дополнение к методу наименьших квадратов и использованию для оценивания суммы модулей отклонений (см. выше), является метод взвешенных наименьших квадратов. Обычный метод наименьших квадратов предполагает, что разброс остатков одинаковый при всех значениях независимых переменных. Иными словами, предполагается, что дисперсия ошибки при всех измерениях одинакова. Часто, это предположение не является реалистичным. В частности, отклонения от него встречаются в бизнесе, экономике, приложениях в биологии (отметим, что оценки параметров по методу взвешенных наименьших квадратов могут быть также получены с помощью модуля Множественная регрессия).

Например, вы хотите изучить связь между проектной стоимостью постройки здания и суммой реально потраченных средств. Это может оказаться полезным для получения оценки ожидаемых перерасходов. В этом случае разумно предположить, что абсолютная величина перерасходов (выраженная в долларах) пропорциональна стоимости проекта. Поэтому, для подбора линейной регрессионной модели следует использовать метод взвешенных наименьших квадратов. Функция потерь может быть, например, такой (см. книгу Neter, Wasserman, and Kutner, 1985, стр.168):

Потери = (наблюд.-предск.)2 * (1/x2)

В этом уравнении первая часть функции потерь означает стандартную функцию потерь для метода наименьших квадратов (наблюдаемые минус предсказанные в квадрате; т.е., квадрат остатков), а вторая равна “весу” этой потери в каждом конкретном случае - единица деленная на квадрат независимой переменной (x) для каждого наблюдения. В ситуации реального оценивания, программа просуммирует значения функции потерь по всем наблюдениям (например, конструкторским проектам), как описано выше и подберет параметры, минимизирующие сумму. Возвращаясь к рассмотренному примеру, чем больше проект (x), тем меньше для нас значит одна и та же ошибка в предсказании его стоимости. Этот метод дает более устойчивые оценки для параметров регрессии (более подробно, см.

Neter, Wasserman, and Kutner, 1985).

Метод максимума правдоподобия.

Метод максимума правдоподобия.

Альтернативой использования метода наименьших квадратов (см выше) является поиск максимума функции правдоподобия или ее логарифма. Эквивалентным способом является минимизация логарифма функции правдоподобия со знаком минус (термин максимум правдоподобия впервые был использован в работе Фишера - Fisher, 1922a). В общем виде, функцию правдоподобия определяется так: L = F(Y,Модель) =

in= 1 {p [yi, Параметры модели(xi)]}

Теоретически, вы можете вычислить вероятность принятия зависимой переменной определенных значений(обозначенную нами L, от слова Likelihood - правдоподобие), используя соответствующую регрессионную модель. Воспользовавшись тем, что все наблюдения независимы друг от друга, получим, что наша функция правдоподобия равна геометрической сумме (

, для всех i = 1 to n) вероятностей конкретных наблюдений (i), заданных соответствующей значению x моделью и параметрами. (Геометрическая сумма означает, что нужно перемножить вероятности по всем возможным случаям внутри скобок.) Часто эти функции представляют в виде натурального логарифма, в этом случае геометрическая сумма становится обычной арифметической суммой (

, для всех i = 1 to n).

При выборе конкретной модели, чем больше правдоподобие модели, тем больше вероятность, что предсказанное значение зависимой переменной окажется в выборке. Поэтому, чем больше правдоподобие, тем лучше модель согласуется с выборочными данными. Реальные вычисления для конкретной модели могут оказаться достаточно громоздкими, поскольку вам необходимо “отслеживать” (вычислять) вероятности появления различных значений зависимой переменной y (выбрав модель и соответствующее значение x). Оказывается, что если все предположения для стандартной множественной регрессии выполнены (они описаны в главе Множественная регрессия руководства пользователя), то стандартный метод наименьших квадратов (см. выше) дает те же оценки, что и метод максимума правдоподобия.

Если предположение о постоянстве дисперсии ошибки при всех значения независимой переменной нарушено, то оценки по методу максимума правдоподобия можно получить используя метод взвешенных наименьших квадратов.

Максимум правдоподобия и пробит/логит модели.

Максимум правдоподобия и пробит/логит модели.

Рассмотрим функцию правдоподобия для регрессионных моделей логит и пробит. Функция потерь для этих моделей вычисляется как сумма натуральных логарифмов логит или пробит правдоподобия L1: log(L1) =

in= 1 [yi*log(pi ) + (1-yi )*log(1-pi )]

где
log(L1) натуральный логарифм функции правдоподобия для выбранной (логит или пробит) модели
yi - i-ое наблюдаемое значение
pi вероятность появления (предсказанная или подогнанная) (между 0 и 1)

Логарифм функции правдоподобия для нулевой модели (L0), т.е. модели, содержащей только свободный член (и не включающей других коэффициентов регрессии) вычисляется как:

log(L0) = n0*(log(n0/n)) + n1*(log(n1/n))

где
log(L0) натуральный логарифм функции правдоподобия для нулевой (логит или пробит) модели
n0 число наблюдений со значением 0
n1 число наблюдений со значением 1
n общее число наблюдений

Алгоритмы минимизации функций

Алгоритмы минимизации функций

. Теперь, после обсуждения различных регрессионных моделей и функций потерь, используемых для их оценки, единственное, что осталось “в тайне”, это как находить минимумы функций потерь (т.е. наборы параметров, наилучшим образом соответствующие оцениваемой модели), и как вычислять стандартные ошибки оценивания параметров. Нелинейное оценивание использует очень эффективный (квази-ньютоновский) алгоритм, который приближенно вычисляет вторую производную функции потерь и использует ее при поиске минимума (т.е., при оценке параметров по соответствующей функции потерь). Кроме того, Нелинейное оценивание предлагает несколько более общих алгоритмов поиска минимума, использующих различные стратегии поиска (не связанные с вычислением вторых производных). Эти стратегии иногда более эффективны при оценивании функций потерь с локальными минимумами; поэтому, эти методы часто очень полезны для нахождения начальных значений с помощью квази-ньютоновского метода. Во всех случаях, вы можете вычислить стандартные ошибки оценок параметров.

Эти вычисления проводятся с использованием частных производных второго порядка по параметрам, которые приближенно подсчитываются с использованием метода конечных разностей.

Если вас интересует, не как именно происходит минимизация функции потерь, а только то, что такая минимизация в принципе возможна, вы можете пропустить следующие разделы. Однако они могут пригодиться, если получаемая регрессионная модель будет плохо согласовываться с данными. В этом случае, итеративная процедура может не сойтись, выдавая неожиданные (например, очень большие или очень маленькие) оценки для параметров.

В следующих параграфах, мы сначала рассмотрим некоторые вопросы, относящиеся к оптимизации без ограничений, затем дадим краткий обзор методов используемых в этом модуле. Более подробное обсуждение этих методов имеется в книгах Brent (1973), Gill and Murray (1974), Peressini, Sullivan, and Uhl (1988), и Wilde and Beightler (1967). Более широкий обзор алгоритмов можно найти в книгах Dennis and Schnabel (1983), Eason and Fenton (1974), Fletcher (1969), Fletcher and Powell (1963), Fletcher and Reeves (1964), Hooke and Jeeves (1961), Jacoby, Kowalik, and Pizzo (1972), и Nelder and Mead (1964).

Начальные значения, размеры шагов и критерии сходимости

Начальные значения, размеры шагов и критерии сходимости

. Общим моментом всех методов оценивания является необходимость задания пользователем некоторых начальных значений, размера шагов и критерия сходимости алгоритма. Все методы начинают свою работу с особого набора предварительных оценок (начальных значений), которые в дальнейшем последовательно уточняются от итерации к итерации. При первой итерации размер шага определяет, как сильно будут меняться параметры. Наконец, критерий сходимости определяет, когда итерационный процесс можно прекратить. Например, процесс итераций можно остановить, когда изменение функции потерь на каждом шаге становится меньше определенной величины.

Штрафные функции, ограничение параметров. Все процедуры Нелинейного оценивания не имеют встроенных ограничений на область поиска.

Это означает, что программа будет изменять значения параметров вне зависимости от допустимости получаемых значений. Например, в ходе логит регрессии оцениваемое значение можете получиться равным 0.0. В этом случае мы не можем вычислить логарифм (поскольку логарифм нуля не определен). В этой ситуации программа автоматически присваивает функции потерь штрафное значение, т.е. очень большое значение. В результате, оценивающие процедуры остаются внутри допустимого диапазона. Однако, в некоторых случаях, процесс оценивания зацикливается, и в результате, мы получаем огромное значение функции потерь. Это может случиться, например, если, если регрессионное уравнение включает взятие логарифма от независимой переменной, которая в некоторых случаях может принимать нулевое значение (в этом случае возникают проблемы с логарифмированием). Для того, чтобы определить ограничения на область изменения параметров, следует добавить к функции потерь некоторую штрафную функцию, равную нулю при допустимых значениях параметра и очень большую при недопустимых. Ниже приведен пример определенной пользователем регрессии и функции потерь, включающий наложение штрафа, если хотя бы один из параметров a или b меньше или равен нуля:

Оцениваемая функция: v3 = a + b*v1 + (c*v2)
Функция потерь: L = (obs - pred)**2 + (a<0)*100000 + (b<0)*100000

Локальные минимумы.

Локальные минимумы.

Самой неприятной проблемой при минимизации функции без ограничений являются локальные минимумы. Например, при небольшом смещении значения параметра в любом направлении функция потерь почти не изменяется. Однако если мы передвинем параметр в совершенно другую область, значение функции потерь может существенно уменьшиться. Вы можете представлять себе такие локальные минимумы как небольшие впадины на графике функции потерь. Однако в большинстве практических приложений локальные минимумы приводят к неправдоподобно большим или неправдоподобно малым значениям параметров с очень большими стандартными ошибками. В этих случаях следует задать другие начальные данные и повторить поиск минимума еще раз.

Отметим также, что симплекс - метод (см. ниже) нечувствителен к таким минимумам, поэтому, он может быть использован для отыскания подходящих начальных значений для сложных функций.

Квази-ньютоновский метод. Как вы, наверное, помните, угловой коэффициент - тангенс угла наклона графика функции в конкретной точке равен производной этой функции (в этой точке), а скорость его изменения в выбранной точке равна второй производной функции в этой точке. Квази-ньютоновский метод вычисляет значения функции в различных точках для оценивания первой и второй производной, используя эти данные для определения направления изменения параметров и минимизации функции потерь.

Симплекс-метод. Этот алгоритм не использует производные функции потерь. Вместо этого, при каждой итерации функция оценивается в m+1 точках m-мерного пространства. Например, на плоскости (т.е., при оценивании двух параметров) программа будет вычислять значение функции потерь в трех точках в окрестности текущего минимума. Эти три точки определяют треугольник; в многомерном пространстве. Получаемая фигура называется симплекс. Интуитивно понятно, что в двумерном пространстве три точки позволяют выбрать “в каком направлении двигаться”, т.е., в каком направлении на плоскости менять параметры для минимизации функции. Похожие принципы применимы в многомерном параметрическом пространстве; т.е., симплекс будет постепенно “смещаться вниз по склону”, в сторону минимизации функции потерь; если же текущий шаг окажется слишком большим для определения точного направления спуска, (т.е., симплекс слишком большой), процедура произведет уменьшение симплекса и продолжит вычисления. Дополнительное преимущество симплекс-метода в том, что при нахождении минимума симплекс снова увеличивается для проверки: не является ли этот минимум локальным. Таким образом, симплекс движется по поверхности по направлению к минимуму функции подобно простому, одноклеточному, организму, уменьшаясь и увеличиваясь при обнаружении локальных минимумов и “гребней”.

Метод Хука-Дживиса.

Метод Хука-Дживиса.

В некотором смысле, это простейший из всех алгоритмов. При каждой итерации метод сначала определяет схему расположения параметров, оптимизируя текущую функцию потерь перемещением каждого параметра по отдельности. При этом вся комбинация параметров сдвигается на новое место. Это новое положение в m-мерном пространстве параметров определяется экстраполяцией вдоль линии, соединяющей текущую базовую точку с новой точкой. Размер шага этого процесса постоянно меняется для попадания в оптимальную точку. Этот метод обычно очень эффективен и его следует использовать, если квази-ньютоновский и симплекс-метод (см. выше) не дали удовлетворительных оценок.

Метод Розенброка. Даже если все остальные методы не сработали, метод Розенброка часто приводит к правильному результату. Этот метод вращает пространство параметров, располагая одну ось вдоль “гребня” поверхности (этот метод также называется метод вращения координат), при этом все другие остаются ортогональными выбранной оси. Если поверхность графика функции потерь имеет одну вершину и различимые “гребни” в направлении минимума функции потерь, этот метод приводит к очень точным значениям параметров, минимизирующим функцию потерь. Однако следует отметить, что этот поисковый алгоритм остановится преждевременно, если на область значений параметров наложены несколько ограничений (отражающихся в штрафном значении; см. выше), которые пересекаются, приводя к обрыванию “гребня”.

Матрица Гессе и стандартные ошибки. Матрицу частных производных второго порядка также часто называют матрицей Гессе. Оказывается, что обратная к ней матрица приблизительно равна матрице ковариаций оцениваемых параметров. Интуитивно понятно, что существует обратная зависимость между производными второго порядка по параметрам и их стандартными ошибками. Если изменить угловой коэффициент в точке минимума функции и сделать минимум функции более “резким”, то производные второго порядка увеличатся; при этом, оценки параметров будут практически стабильными в смысле, что параметры в точке минимума будут легко уточняемы.

Если же производная второго порядка будет близка к нулю, то угол наклона в точке минимума будет практически неизменным, приводя к тому, что вы можете двигать параметры практически в любом направлении почти не изменяя значение функции потерь. Поэтому стандартные ошибки параметров будут очень большими. Матрица Гессе и асимптотические стандартные ошибки для параметров вычисляются отдельно методом конечных разностей. Эта процедура возвращает очень точные асимптотические стандартные ошибки для всех методов оценивания.

В начало

Оценивание пригодности модели
Оценивание пригодности модели

После оценивания регрессионных параметров, существенной стороной анализа является проверка пригодности модели в целом. Например, если вы определили линейную регрессионную модель, а реальная зависимость переменных по своей природе нелинейна, то оценки параметров (коэффициентов регрессии) и оценки стандартных ошибок этих приближений могут оказаться совершенно неудовлетворительными. Рассмотрим некоторые методы проверки пригодности модели.

Объясненная доля дисперсии
Критерий согласия хи-квадрат
График наблюдаемых и предсказанных значений
Нормальный и полунормальный график остатков
График функции подгонки
Ковариационная матрица оценок параметров

Объясненная доля дисперсии.
Объясненная доля дисперсии.

Вне зависимости от рассматриваемой модели, мы всегда можем оценить полную дисперсию зависимой переменной (полную сумму квадратов - total sum of squares, SST), долю дисперсии, приходящейся на остатки (сумму квадратов ошибок - error sum of squares, SSE), и долю дисперсии относительно регрессионной модели (сумму квадратов относительно регрессии - regression sum of squares, SSR = SST - SSE). Отношение суммы квадратов относительно регрессии к полной сумме квадратов (SSR/SST) обозначается термином объясненная доля дисперсии зависимой переменной (y) в регрессионной модели. Таким образом, эта доля эквивалентна значению R-квадрат (0

R-квадрат

1, так называемому квадрату смешанной корреляции (коэффициенту определенности- coefficient of determination в англоязычной литературе)).

Даже если распределение зависимой переменной не является нормальным, это отношение помогает оценить, насколько хорошо подобранная модель согласуется с исходными данными.

Критерий согласия хи-квадрат.

Критерий согласия хи-квадрат.

Для регрессионных моделей пробит и логит, Нелинейное оценивание использует оценивание по методу максимума правдоподобия (т.е. максимизирует функцию правдоподобия). Но оказывается, что можно непосредственно сравнить правдоподобие L0 нулевой модели, где все параметры наклона равны нулю, с правдоподобием L1 подогнанной модели. А именно, можно вычислить значение статистики хи-квадрат для нашего отношения по формуле: Хи-квадрат = -2 * (log(L0) - log(L1))

Число степеней свободы для этого значения хи-квадрат равно разности числа параметров для подогнанной и числа параметров для нулевой моделей, поэтому число степеней свободы будет равно числу независимых переменных в подогнанной логит или пробит регрессии. Если p-уровень, соответствующий этому значению хи-квадрат, является значимым, то вы можете сказать, что оцениваемая модель значительно лучше соответствует данным, чем нулевая модель, т.е. параметры регрессии статистически значимы.

График наблюдаемых и предсказанных значений.

График наблюдаемых и предсказанных значений.

При проведении исследований часто полезным бывает использование диаграммы рассеяния наблюдаемых и предсказанных значений. Если модель хорошо соответствует данным, можно ожидать, что точки расположатся вдоль прямой линии, если же модель задана неправильно, то полученная из точек на графике фигура будет мало похожа на прямую линию.

Нормальный и полунормальный графики остатков. Нормальный вероятностный график остатков показывает насколько распределение остатков (ошибок) близко к нормальному.

График функции подгонки. Для моделей, включающих две или три переменные (один или два предиктора) полезно строить функцию подгонки с использованием окончательных оценок параметров. Посмотрите на пример 3М графика с двумя предикторными переменными:

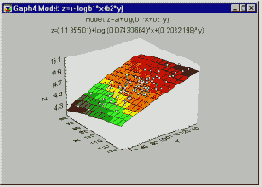
Этот тип графика предоставляет хорошую возможность проверить, подходит ли модель к данным или нет, и где расположены явные выбросы.

Ковариационная матрица оценок параметров.

Ковариационная матрица оценок параметров.

Если подобранная модель сильно отличается от реальной, или процедура оценивания “застряла” на локальном минимуме, ошибки для оценок параметров могут получиться очень большими. Это означает, что как бы мы не меняли конечные значения параметров, полученная в результате функция потерь практически не изменится. Кроме того, параметры могут оказаться сильно коррелированными. Это говорит о том, что некоторые параметры излишни. Поэтому изменение функции потерь при изменении оценивающим алгоритмом полученного значения одного параметра может быть практически скомпенсировано перемещением другого параметра и изучение совместного влияния этих параметров на функцию потерь оказывается излишним.

В начало